PSSFSS Function Reference

PSSFSS.analyze — Function

result = analyze(strata::Vector, flist, steering; outlist=[], logfile="pssfss.log", resultfile="pssfss.res", 
showprogress::Bool=true, fastsweep=true)

Analyze a full FSS/PSS structure over a range of frequencies and steering angles/phasings. Generate output files as specified in outlist.

Positional Arguments

strata: A vector of Layer and Sheet objects. The first and last entries must be of type Layer.
flist: An iterable containing the analysis frequencies in GHz.
steering: A length 2 NamedTuple containing as keys the steering parameter labels and as values the iterables that define the values of steering parameters to be analyzed.
- one of {:phi ,:ϕ} and one of {:theta, :θ}, or
- one of {:psi1 ,:ψ₁} and one of {:psi2, :ψ₂}.
All steering parameters are input in degrees.
The program will analyze while iterating over a triple loop over the two steering parameters and frequency, with frequency in the innermost loop (i.e. varying the fastest). The steering parameter listed first will be in the outermost loop and will therefore vary most slowly.

Keyword Arguments

outlist: A matrix with 2 columns. The first column in each row is a string containing the name of the CSV file to write the output to. The second entry in each row is a tuple generated by the @outputs macro of the Outputs module. The contents of the specified file(s) will be updated as the program completes each analysis frequency.
logfile: A string containing the name of the log file to which timing and other information about the run is written. Defaults to "pssfss.log". If this file already exists, it will be overwritten.
resultfile: A string containing the name of the results file. Defaults to pssfss.res. If this file already exists, it will be overwritten. It is a binary file that contains information (including the generalized scattering matrix) from the analysis performed for each scan condition and frequency. The result file can be post-processed to produce similar or additional outputs that were requested at run time via the outlist argument.
showprogress: If true (default), then show progress bar during execution.
fastsweep: If true (default) use an interpolated fast sweep for each frequency loop.

Return Value

result: A vector of Result objects, one for each scan angle/frequency combination. This

vector can be passed as an input to the extract_result function to obtain any desired performance parameters that are supported by the @outputs macro.

source

PSSFSS.Elements.diagstrip — Function

diagstrip(;P::Real, w::Real, orient::Real, Nl::Int, Nw::Int, units::PSSFSSLength, kwargs...)

Return a variable of type RWGSheet that contains the triangulation for a rectangular strip inside a square unit cell, with the strip centerline coincident with one of the diagonals of the cell. The strip runs the full length of the diagonal.

Arguments:

All arguments are keyword arguments which can be entered in any order.

Required arguments:

P: The period (i.e. side length) of the square unit cell. Note that the center-center spacing of the strips is P/√2.
w: The width of the strip.
orient: The orientation of the strip within the unrotated unit cell in degrees. The only valid values are 45 for a strip running from lower left to upper right and -45 for a strip running from lower right to upper left.
units: Length units (mm, cm, inch, or mil)
Nl and Nw: Number of line segments along the length and width of the strip, for dividing up the strip into rectangles, which are triangulated by adding a diagonal to each rectangle. These arguments are actually used for triangulating the central, rectangular portion of the strip. The ends of the strip are tapered in the form of right, isosceles triangles, to conform to the boundaries of the square unit cell. These triangular "end-caps" are triangulated using an unstructured mesh.

Optional arguments:

class::Char='J' Specify the class, either 'J' or 'M'.. If 'J', the unknowns are electric surface currents, as used to model a wire or metallic patch-type FSS. If 'M', the unknowns are magnetic surface currents, as used to model a slot or aperture in a perfectly conducting plane.
dx::Real=0.0, dy::Real=0.0: These specify the offsets in the x and y directions applied to the entire unit cell and its contents. Length units are as specified in the units keyword.
rot::Real=0.0: Counterclockwise rotation angle in degrees applied to the entire unit cell and its contents. This rotation is applied prior to any offsets specified in dx and dy.
Zsheet::Complex=0.0: The frequency-independent surface impedance of the FSS conductor in units of [Ω]. May only be specified for a sheet of class 'J'. If Zsheet is specified, then sigma (or σ) may not be specified. )
sigma or σ: DC, bulk conductivity [S/m]. Only allowed for sheets of class 'J'. Cannot be simultaneously specified with Zsheet. Is used with Rq by PSSFSS to calculate an effective sheet surface impedance at each frequency, using the Gradient Model (Grujić 2022).
Rq=0.0: RMS surface roughness [m]. Only legal for class 'J'. Only used if sigma (or σ) is also specified. In that case is is used along with sigma to calculate a frequency-dependent sheet impedance using the Gradient Model. The default value of 0 denotes a smooth surface.
disttype::Symbol=:normal: Probability distrubution type for surface roughness. defaults to :normal. The other legal value is :rayleigh.
fufp::Bool: This keyword is not usually required. fufp is mnemonic for "Find Unique Face Pairs". If true, the code will search the triangulation for classes of triangle pairs that are the equivalent in the toeplitz sense. I.e., if triangle pairs (A,B) and (C,D) belong to the same equivalence class, the six vertices in the pair (A,B) can be made to coincide with those of pair (C,D) by a simple translation. If there are many such equivalent pairs, a significant decrease in matrix fill time ensues by exploiting the equivalence. The tradeoff is the time needed to identify them. The default value is true for the strip, diagstrip, meander, manji, loadedcross, jerusalemcross, and 4-sided polyring styles (those employing structured meshes) and false for the remaining styles (those employing unstructured meshes).
save::String="" Specifies a file name to which the sheet triangulation and unit cell data is to be written, typically to be plotted later.

source

PSSFSS.Sheets.edgecount — Function

edgecount(s::RWGSheet)

Return the number of triangle edges in the RWGSheet triangulation.

source

PSSFSS.Sheets.export_sheet — Function

export_sheet(fname::AbstractString, sheet::RWGSheet, export_type)

Export an RWGSheet triangulation to an STL CAD file. export_type may be either STL_ASCII or STL_BINARY.

source

PSSFSS.Outputs.extract_result — Function

extract_result(r::Result, ops::NTuple{N,Outfun}) --> Row Matrix
extract_result(r::AbstractVector{Result}, ops::NTuple{N,Outfun}) --> Matrix

Return a matrix of outputs extracted from a Result instance or vector. ops is a NTuple as returned by the @outputs macro.

Example

results = analyze(...)
ops = @outputs FGHz s11dB(h,h) s11ang(h,h)
data = extract_result(results, ops)
# or data = extract_result(results[1], ops) # returns a single row

source

extract_result(fname::AbstractString, ops::Tuple) --> Matrix

Return a matrix of outputs extracted from a results file. ops is a Tuple returned by the @outputs macro.

Example

ops = @outputs FGHz S11DB(H,H) S11ANG(H,H)
data = extract_result("pssfss.res", ops)

source

PSSFSS.Sheets.facecount — Function

facecount(s::RWGSheet)

Return the number of triangle faces in the RWGSheet triangulation.

source

PSSFSS.Elements.jerusalemcross — Function

jerusalemcross(;P::Real, L1::Real, L2::Real, A::Real, B::Real, w::Real, 
             ntri::Int, units::PSSFSSLength, kwargs...)

Description:

Create a variable of type RWGSheet that contains the triangulation for a "Jerusalem cross" type of geometry. The returned value has fields s₁, s₂, β₁, β₂, ρ, e1, e2, fv, fe, and fr properly initialized.

The following "ascii art" attempts to show the definitions of the geometrical parameters P, L1, L2, A, B, and w. Note that the structure is supposed to be symmetrical wrt reflections about its horizontal and vertical centerlines, and wrt reflections through a line oriented at a 45 degree angle wrt the x-axis.

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓ 
┃                                                       ┃ _______
┃               ┌────────────────────────┐              ┃    ↑
┃               │ ┌───────────────────┐  │              ┃    │
┃               │ └───────┐    ┌──────┘  │              ┃    │
┃               └──────┐  │    │ ┌───────┘              ┃    │
┃                      │  │    │ │                      ┃    │
┃  ┌───────┐           │  │    │ │            ┌──────┐  ┃    │
┃  │  ┌─┐  │           │  │    │ │            │ ┌──┐ │  ┃    │
┃  │  │ │  │           │  │   →│ │← w         │ │  │ │  ┃    │
┃  │  │ │  │           │  │    │ │            │ │  │ │  ┃    │
┃  │  │ │  └───────────┘  │    │ └────────────┘ │  │ │  ┃    │
┃  │  │ └─────────────────┘    └────────────────┘  │ │  ┃    
┃  │  │                                            │ │  ┃   L1 
┃  │  │ ┌─────────────────┐    ┌────────────────┐  │ │  ┃  
┃  │  │ │  ┌───────────┐  │    │ ┌────────────┐ │  │ │  ┃    │
┃  │  │ │  │           │  │    │ │            │ │  │ │  ┃    │
┃  │  │ │  │           │  │    │ │            │ │  │ │  ┃    │
┃  │  └─┘  │          →│  │    │ │← L2     B →│ └──┘ │← ┃    │
┃  └───────┘           │  │    │ │            └──────┘  ┃    │
┃                      │  │    │ │                      ┃    │
┃               ┌──────┘  │    │ └───────┐              ┃    │
┃               │ ┌───────┘    └──────┐  │              ┃    │
┃               │ └───────────────────┘  │              ┃    │
┃               └────────────────────────┘              ┃ ___↓___
┃               |<───────── A ──────────>|              ┃
┗━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┛ 
|<─────────────────────── P ───────────────────────────>|

Arguments:

All arguments are keyword arguments which can be entered in any order.

Required arguments:

P: The period, i.e. the side length of the square unit cell.
L1,L2, A, B, w: Geometrical parameters as defined above. Note that it is permissible to specify w ≥ L2/2 and/or w ≥ B/2 in which case the respective region will be filled in solidly with triangles. If both conditions hold, then the entire structure will be filled in (i.e., singly-connected). In that case the L2 and B dimensions will be used for the respective widths of the arms, and w will not be used.
units: Length units (mm, cm, inch, or mil)
ntri: The desired total number of triangles. This is a guide/request, the actual number will likely be different.

Optional arguments:

class::Char='J' Specify the class, either 'J' or 'M'.. If 'J', the unknowns are electric surface currents, as used to model a wire or metallic patch-type FSS. If 'M', the unknowns are magnetic surface currents, as used to model a slot or aperture in a perfectly conducting plane.
dx::Real=0.0, dy::Real=0.0: These specify the offsets in the x and y directions applied to the entire unit cell and its contents. Length units are as specified in the units keyword.
rot::Real=0.0: Counterclockwise rotation angle in degrees applied to the entire unit cell and its contents. This rotation is applied prior to any offsets specified in dx and dy.
Zsheet::Complex=0.0: The frequency-independent surface impedance of the FSS conductor in units of [Ω]. May only be specified for a sheet of class 'J'. If Zsheet is specified, then sigma (or σ) may not be specified. )
sigma or σ: DC, bulk conductivity [S/m]. Only allowed for sheets of class 'J'. Cannot be simultaneously specified with Zsheet. Is used with Rq by PSSFSS to calculate an effective sheet surface impedance at each frequency, using the Gradient Model (Grujić 2022).
Rq=0.0: RMS surface roughness [m]. Only legal for class 'J'. Only used if sigma (or σ) is also specified. In that case is is used along with sigma to calculate a frequency-dependent sheet impedance using the Gradient Model. The default value of 0 denotes a smooth surface.
disttype::Symbol=:normal: Probability distrubution type for surface roughness. defaults to :normal. The other legal value is :rayleigh.
fufp::Bool: This keyword is not usually required. fufp is mnemonic for "Find Unique Face Pairs". If true, the code will search the triangulation for classes of triangle pairs that are the equivalent in the toeplitz sense. I.e., if triangle pairs (A,B) and (C,D) belong to the same equivalence class, the six vertices in the pair (A,B) can be made to coincide with those of pair (C,D) by a simple translation. If there are many such equivalent pairs, a significant decrease in matrix fill time ensues by exploiting the equivalence. The tradeoff is the time needed to identify them. The default value is true for the strip, diagstrip, meander, manji, loadedcross, jerusalemcross, and 4-sided polyring styles (those employing structured meshes) and false for the remaining styles (those employing unstructured meshes).
save::String="" Specifies a file name to which the sheet triangulation and unit cell data is to be written, typically to be plotted later.
structuredtri::Bool=true: If true, use a structured mesh for the triangulation. If false, the unstructured mesh generator that was standard up to PSSFSS version 1.2 will be used. A structured mesh can be analyzed more efficiently, but the number of triangles created by the unstructured mesh generator is usually closer to ntri than the number for the structured mesh generator.

source

PSSFSS.Layers.Layer — Type

Layer <: Any

An instance of the Layer type represents a single dielectric layer of the physical structure. It contains the electrical properties of the dielectric layer. For layers not included in a Gblock, an instance of Layer also specifies the periodicity (via the reciprocal lattice vectors) and stores the mode constants for the Floquet modes present in the layer.

Layer(;width::0mm, ϵᵣ=1.0, tanδ=0.0, μᵣ=1.0, mtanδ=0.0)
Layer(;width::0mm, epsr=1.0, tandel=0.0, mur=1.0, mtandel=0.0)

Create a Layer instance with the specified electrical properties. All arguments are optional keyword arguments with default values as shown above. They can be supplied in any order. Typically the first and last Layer in a composite FSS or PSSFSS structure are generated by a call to Layer() to represent the semi-infinite vacuum regions surrounding the structure. Using the default width of 0mm means that the phase reference planes are located at the surfaces just adjacent to these semi-infinite end Layers.

Arguments

width: The layer width (i.e. thickness) expressed as a Unitful length quantity. For convenience the following unit suffixes are exported by this module: m, cm, mil, inch, so one can specify, e.g., width=20mil. Note that width can be negative for the first and/or final layer of the composite structure, which has the effect of shifting the phase reference plane towards the interior of the composite structure. This is sometimes needed when interfacing with other programs, such as TEP file generation for Ticra's GRASP program.
ϵᵣ or epsr: Relative permittivity of the dielectric.
tanδ or tandel: Loss tangent (electrical) of the dielectric.
μᵣ or mur: Relative permeability of the dielectric.
mtanδ or mtandel: Loss tangent (magnetic) of the dielectric.

source

PSSFSS.Elements.loadedcross — Function

loadedcross(;s1::Vector{<:Real}, s2::Vector{<:Real}, L1::Real, L2::Real, w::Real, 
             ntri::Int, units::PSSFSSLength, kwargs...)

Description:

Create a variable of type RWGSheet that contains the triangulation for a "loaded cross" type of geometry. The returned value has fields s₁, s₂, β₁, β₂, ρ, e1, e2, fv, fe, and fr properly initialized.

The following (very poor) "ascii art" attempts to show the definitions of the geometrical parameters L1, L2 and w. Note that the structure is supposed to be symmetrical wrt reflections about its horizontal and vertical centerlines, and wrt reflections through a line oriented at a 45 degree angle wrt the x-axis.

 ^                 ----------------
 |                 |  _________   |
 |                 |  |       |   |
 |                 |  |       |   |
 |                 |  |    -->|   |<--- W
 |                 |  |       |   |
 |                 |  |       |   |
 |     ------------   |       |   -------------
 |     |  |-----------|       |------------|  |
 |     |  |                                |  |
 L1    |  |                                |  |
 |     |  |                                |  |
 |     |  |                                |  |
 |     |  ------------          ------------  |
 |     |-----------   |        |  ------------|
 |                 |  |        |  |
 |                 |  |        |  |
 |                 |  |        |  |
 |                 |  |        |  |
 |                 |  |________|  |
 |                 |              |
 V                 ----------------

                   <---- L2 ------>

Arguments:

All arguments are keyword arguments which can be entered in any order.

Required arguments:

s1 and s2: 2-vectors containing the unit cell lattice vectors.
L1,L2,w: Geometrical parameters as defined above. Note that it is permissible to specify w ≥ L2/2 in which case a solid (i.e., singly-connected) cross will be generated. In that case the L2 dimension will be used for the width of the cross pieces.
units: Length units (mm, cm, inch, or mil)
ntri: The desired total number of triangles. This is a guide/request, the actual number will likely be different.

Optional arguments:

orient::Real=0.0: Counterclockwise rotation angle in degrees used to locate the initial vertex of the loaded cross. The default is to locate the vertex on the positive x-axis.
class::Char='J' Specify the class, either 'J' or 'M'.. If 'J', the unknowns are electric surface currents, as used to model a wire or metallic patch-type FSS. If 'M', the unknowns are magnetic surface currents, as used to model a slot or aperture in a perfectly conducting plane.
dx::Real=0.0, dy::Real=0.0: These specify the offsets in the x and y directions applied to the entire unit cell and its contents. Length units are as specified in the units keyword.
rot::Real=0.0: Counterclockwise rotation angle in degrees applied to the entire unit cell and its contents. This rotation is applied prior to any offsets specified in dx and dy.
Zsheet::Complex=0.0: The frequency-independent surface impedance of the FSS conductor in units of [Ω]. May only be specified for a sheet of class 'J'. If Zsheet is specified, then sigma (or σ) may not be specified. )
sigma or σ: DC, bulk conductivity [S/m]. Only allowed for sheets of class 'J'. Cannot be simultaneously specified with Zsheet. Is used with Rq by PSSFSS to calculate an effective sheet surface impedance at each frequency, using the Gradient Model (Grujić 2022).
Rq=0.0: RMS surface roughness [m]. Only legal for class 'J'. Only used if sigma (or σ) is also specified. In that case is is used along with sigma to calculate a frequency-dependent sheet impedance using the Gradient Model. The default value of 0 denotes a smooth surface.
disttype::Symbol=:normal: Probability distrubution type for surface roughness. defaults to :normal. The other legal value is :rayleigh.
fufp::Bool: This keyword is not usually required. fufp is mnemonic for "Find Unique Face Pairs". If true, the code will search the triangulation for classes of triangle pairs that are the equivalent in the toeplitz sense. I.e., if triangle pairs (A,B) and (C,D) belong to the same equivalence class, the six vertices in the pair (A,B) can be made to coincide with those of pair (C,D) by a simple translation. If there are many such equivalent pairs, a significant decrease in matrix fill time ensues by exploiting the equivalence. The tradeoff is the time needed to identify them. The default value is true for the strip, diagstrip, meander, manji, loadedcross, jerusalemcross, and 4-sided polyring styles (those employing structured meshes) and false for the remaining styles (those employing unstructured meshes).
save::String="" Specifies a file name to which the sheet triangulation and unit cell data is to be written, typically to be plotted later.
structuredtri::Bool=true: If true, use a structured mesh for the triangulation. If false, the unstructured mesh generator that was standard up to PSSFSS version 1.2 will be used. A structured mesh can be analyzed more efficiently, but the number of triangles created by the unstructured mesh generator is usually closer to ntri than the number for the structured mesh generator.

source

PSSFSS.Elements.manji — Function

function manji(; L1, L2, L3, w, s1, s2, ntri, units, a=0, w2=0, CCW=false, orient=0, kwargs...)

Description:

Create a variable of type RWGSheet that contains the triangulation for a "manji" (Japanese for swastica shape) type of geometry. The returned value has fields s₁, s₂, β₁, β₂, ρ, e1, e2, fv, fe, and fr properly initialized.

Arguments:

All arguments are keyword arguments which can be entered in any order.

Required arguments:

L1, L2, L3, w: Geometrical parameters defined in the diagram at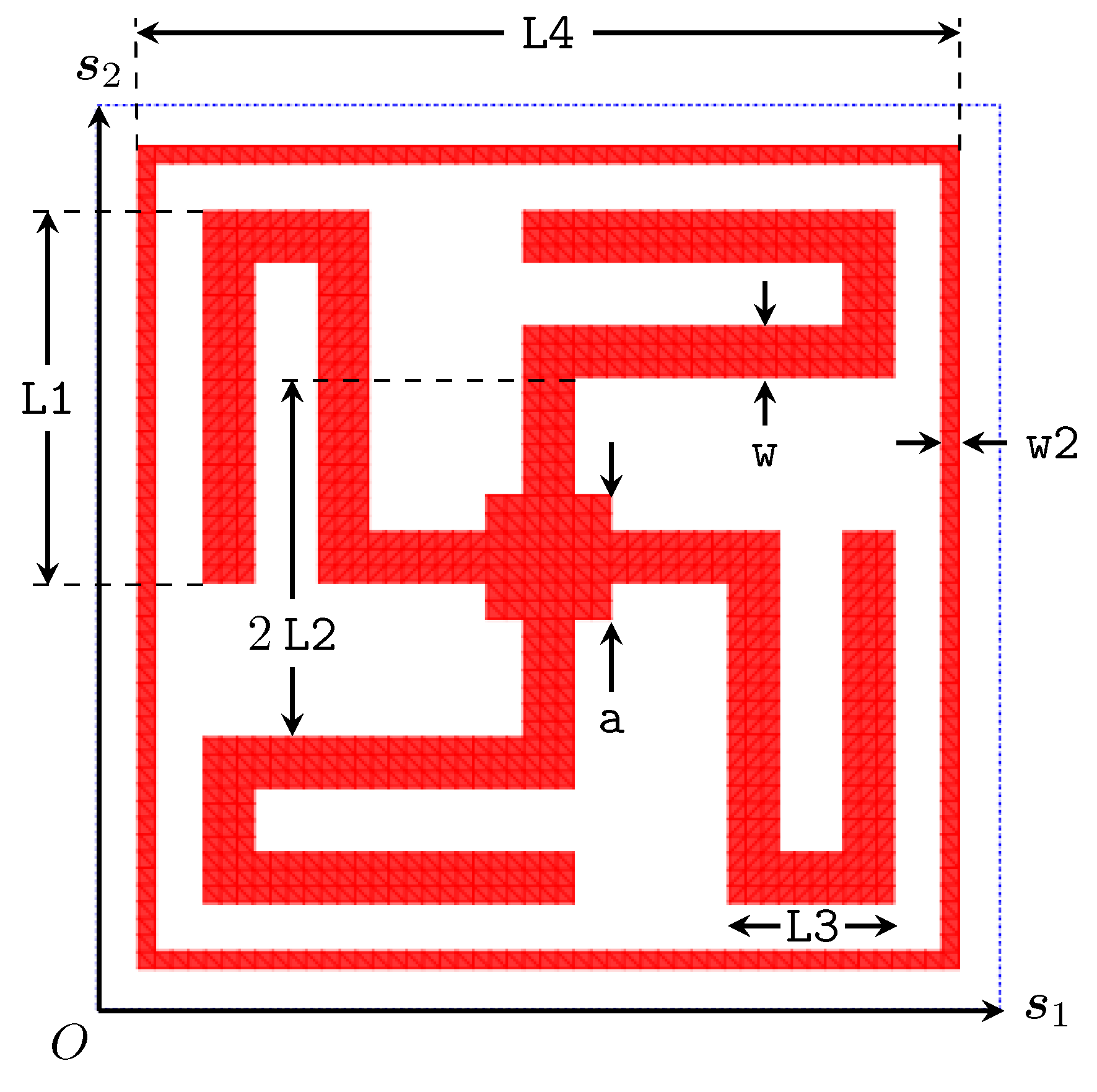 Note that if a ≤ w then the center square shown in the figure will not be present. Similarly, if L3 ≤ 2*w then the bent portions of the arms will consist of a single strip of width L3 (without any gap in the middle).
s1 and s2: 2-vectors containing the unit cell lattice vectors.
units: Length units (mm, cm, inch, or mil)
ntri: The desired total number of triangles. This is a guide/request, the actual number will likely be different.

Optional arguments:

a::Real=0: A geometrical parameter defined in the above referenced diagram. If a ≤ w then the center square shown in that figure will be absent, and the arms will continue uninterrupted to the center of the structure.
w2::Real=0: The width of the square ring border shown in the above-referenced diagram. If w2 ≤ 0 the square ring will not be included in the triangulation. Note that w2 > 0 is only allowed for square unit cells.
L4: The outer side length of the square ring border. 0 < L4 ≤ norm(s1). If not specified, when w2 > 0, the default value for L4 is the unit cell square dimension. It is the user's responsibility to ensure that L4 is large enough to prevent the square ring from interfering with other parts of the manji structure.
CCW::Bool=false: By default, the chiral structure has a clockwise sense. If CCW is true, the structure will be counter-clockwise.
orient::Real=0.0: Counterclockwise rotation angle in degrees applied to the structure within the unrotated unit cell. Note that the outer square ring present when w2 > 0 will not be rotated by use of a nonzero orient value.
class::Char='J' Specify the class, either 'J' or 'M'.. If 'J', the unknowns are electric surface currents, as used to model a wire or metallic patch-type FSS. If 'M', the unknowns are magnetic surface currents, as used to model a slot or aperture in a perfectly conducting plane.
dx::Real=0.0, dy::Real=0.0: These specify the offsets in the x and y directions applied to the entire unit cell and its contents. Length units are as specified in the units keyword.
rot::Real=0.0: Counterclockwise rotation angle in degrees applied to the entire unit cell and its contents. This rotation is applied prior to any offsets specified in dx and dy.
Zsheet::Complex=0.0: The frequency-independent surface impedance of the FSS conductor in units of [Ω]. May only be specified for a sheet of class 'J'. If Zsheet is specified, then sigma (or σ) may not be specified. )
sigma or σ: DC, bulk conductivity [S/m]. Only allowed for sheets of class 'J'. Cannot be simultaneously specified with Zsheet. Is used with Rq by PSSFSS to calculate an effective sheet surface impedance at each frequency, using the Gradient Model (Grujić 2022).
Rq=0.0: RMS surface roughness [m]. Only legal for class 'J'. Only used if sigma (or σ) is also specified. In that case is is used along with sigma to calculate a frequency-dependent sheet impedance using the Gradient Model. The default value of 0 denotes a smooth surface.
disttype::Symbol=:normal: Probability distrubution type for surface roughness. defaults to :normal. The other legal value is :rayleigh.
fufp::Bool: This keyword is not usually required. fufp is mnemonic for "Find Unique Face Pairs". If true, the code will search the triangulation for classes of triangle pairs that are the equivalent in the toeplitz sense. I.e., if triangle pairs (A,B) and (C,D) belong to the same equivalence class, the six vertices in the pair (A,B) can be made to coincide with those of pair (C,D) by a simple translation. If there are many such equivalent pairs, a significant decrease in matrix fill time ensues by exploiting the equivalence. The tradeoff is the time needed to identify them. The default value is true for the strip, diagstrip, meander, manji, loadedcross, jerusalemcross, and 4-sided polyring styles (those employing structured meshes) and false for the remaining styles (those employing unstructured meshes).
save::String="" Specifies a file name to which the sheet triangulation and unit cell data is to be written, typically to be plotted later.

source

PSSFSS.Elements.meander — Function

meander(;a::Real, b::Real, h::Real, w1::Real, w2::Real, ntri::Int,
              units::PSSFSSLength, orient=0, kwarg...) --> sheet::RWGSheet

Description:

Return a variable of type RWGSheet that contains the triangulation for a meanderline strip. The returned sheet has the components s₁, s₂, β₁, β₂, ρ, e1, e2, fv, fe, and fr properly initialized. Geometrical parameters are shown in the following diagram:

  - - - - - - - - - - - - - - - - - - - - - - - - -             ^
 |                                                |             |
 |                                                |             |
 |                                                |             |
 |                                                |             |
 |                                                |             |
 |            <-------- a/2 ------->              |             |
 |               (center-to-center)               |             |
 |                                                |             |
 |          ----------------------------          |  ^    ^     b
 |          |                          |          |  w2   |     |
 |          |                          |          |  |    |     |
 |          | -----------------------  |          |  v    |     |
 |          | |                     |  |          |             |
 |       -->| |<--w1           w1-->|  |<--       |       h     |
 ------------ |                     |  ------------  ^          |
 |            |                     |             |  w2   |     |
 |            |                     |             |  |    |     |
 ------------ - - - - - - - - - - - ---------------  v    v     v

 <-------------------- a ------------------------->

a and b are unit cell dimensions. w1 and w2 are the widths of the vertical and horizontal strips, resp. h is the total height of the meander.

A nicer diagram: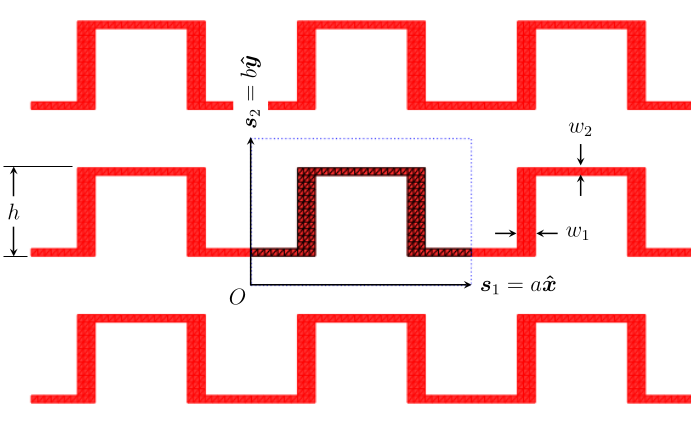

Arguments:

All arguments are keyword arguments which can be entered in any order.

Required arguments:

a,b,h,w1, w2: Geometrical parameters as defined above.
units: Length units (mm, cm, inch, or mil)
ntri: The desired total number of triangles. This is a guide, the actual number will likely be different.

Optional arguments:

orient::Real=0.0: Counterclockwise rotation angle in degrees used to rotate the meanderline orientation within the unrotated unit cell. Nonzero values are allowed only when the unit cell is a square (i.e. a == b). The only allowable values are positive or negative multiples of 90.
class::Char='J' Specify the class, either 'J' or 'M'.. If 'J', the unknowns are electric surface currents, as used to model a wire or metallic patch-type FSS. If 'M', the unknowns are magnetic surface currents, as used to model a slot or aperture in a perfectly conducting plane.
dx::Real=0.0, dy::Real=0.0: These specify the offsets in the x and y directions applied to the entire unit cell and its contents. Length units are as specified in the units keyword.
rot::Real=0.0: Counterclockwise rotation angle in degrees applied to the entire unit cell and its contents. This rotation is applied prior to any offsets specified in dx and dy.
Zsheet::Complex=0.0: The frequency-independent surface impedance of the FSS conductor in units of [Ω]. May only be specified for a sheet of class 'J'. If Zsheet is specified, then sigma (or σ) may not be specified. )
sigma or σ: DC, bulk conductivity [S/m]. Only allowed for sheets of class 'J'. Cannot be simultaneously specified with Zsheet. Is used with Rq by PSSFSS to calculate an effective sheet surface impedance at each frequency, using the Gradient Model (Grujić 2022).
Rq=0.0: RMS surface roughness [m]. Only legal for class 'J'. Only used if sigma (or σ) is also specified. In that case is is used along with sigma to calculate a frequency-dependent sheet impedance using the Gradient Model. The default value of 0 denotes a smooth surface.
disttype::Symbol=:normal: Probability distrubution type for surface roughness. defaults to :normal. The other legal value is :rayleigh.
fufp::Bool: This keyword is not usually required. fufp is mnemonic for "Find Unique Face Pairs". If true, the code will search the triangulation for classes of triangle pairs that are the equivalent in the toeplitz sense. I.e., if triangle pairs (A,B) and (C,D) belong to the same equivalence class, the six vertices in the pair (A,B) can be made to coincide with those of pair (C,D) by a simple translation. If there are many such equivalent pairs, a significant decrease in matrix fill time ensues by exploiting the equivalence. The tradeoff is the time needed to identify them. The default value is true for the strip, diagstrip, meander, manji, loadedcross, jerusalemcross, and 4-sided polyring styles (those employing structured meshes) and false for the remaining styles (those employing unstructured meshes).
save::String="" Specifies a file name to which the sheet triangulation and unit cell data is to be written, typically to be plotted later.

source

PSSFSS.Sheets.nodecount — Function

nodecount(s::RWGSheet)

Return the number of unique triangle vertices in the RWGSheet triangulation.

source

PSSFSS.Outputs.@outputs — Macro

@outputs(args...)

Convert list of user output requests to a vector of functors that generate the requested outputs when applied to a Result instance. In the conversion process, replace lower case letters with upper case.

Examples

julia> output = @outputs FGHz θ ϕ s11db(te,te) S11ang(Te,te)
julia> output = @outputs FGHz theta phi s21db(R,H) ARdB21(H) ARdB11(v)

source

PSSFSS.Elements.pecsheet — Function

pecsheet()

Return a variable of type RWGSheet that contains a perfect electric conducting sheet (i.e. an "E-wall").

source

PSSFSS.Elements.pmcsheet — Function

pmcsheet()

Return a variable of type RWGSheet that contains a perfect magnetic conducting sheet (i.e. an "H-wall").

source

PSSFSS.Elements.polyring — Function

polyring(;s1::Vector, s2::Vector, a::Vector, b::Vector, sides::Int ,ntri::Int ,orient::Real, units::PSSFSSLength, kwargs...) --> RWGSheet

Return a variable of type RWGSheet that contains the triangulation for one or more concentric annular regions bounded by polygons.

Arguments:

All arguments are keyword arguments which can be entered in any order.

Required arguments:

units: Length units (mm, cm, inch, or mil)
s1 and s2: 2-vectors containing the unit cell lattice vectors.
a and b: n-vectors (n>=1) of the same length providing the inner and outer radii, respectively of the polygonal rings. Entries in a and b must be strictly increasing, except for possibly b[end] as discussed below. b[i] > a[i] ∀ i ∈ 1:n, except possibly b[end] as discussed below. a[1] may be zero to denote a solid (non-annular) polygon as the first "ring". It is possible to let the outermost ring to extend completely to the unit cell boundary. This is specified by setting b[end] < 0, in which case for unstructured meshes, -b[end] is interpreted as the number of edges along the shorter of the s1 and s2 lattice vectors.
sides: The number (>= 3) of polygon sides.
ntri: The desired total number of triangles distributed among all the annular regions. This is a guide, the actual number will likely be different.

Optional arguments:

orient::Real=0.0: Counterclockwise rotation angle in degrees used to locate the initial vertex of the polygonal rings. The default is to locate the vertex on the positive x-axis.
structuredtri::Bool: Defaults to true when sides==4 and false otherwise. A true value is only allowed when sides==4 and s1 ⟂ s2. If true, use a structured mesh for the triangulation. If false, the unstructured mesh generator that was standard up to PSSFSS version 1.2 will be used. A structured mesh can be analyzed more efficiently, but the number of triangles created by the unstructured mesh generator is usually closer to ntri than the number for the structured mesh generator.
class::Char='J' Specify the class, either 'J' or 'M'.. If 'J', the unknowns are electric surface currents, as used to model a wire or metallic patch-type FSS. If 'M', the unknowns are magnetic surface currents, as used to model a slot or aperture in a perfectly conducting plane.
dx::Real=0.0, dy::Real=0.0: These specify the offsets in the x and y directions applied to the entire unit cell and its contents. Length units are as specified in the units keyword.
rot::Real=0.0: Counterclockwise rotation angle in degrees applied to the entire unit cell and its contents. This rotation is applied prior to any offsets specified in dx and dy.
Zsheet::Complex=0.0: The frequency-independent surface impedance of the FSS conductor in units of [Ω]. May only be specified for a sheet of class 'J'. If Zsheet is specified, then sigma (or σ) may not be specified. )
sigma or σ: DC, bulk conductivity [S/m]. Only allowed for sheets of class 'J'. Cannot be simultaneously specified with Zsheet. Is used with Rq by PSSFSS to calculate an effective sheet surface impedance at each frequency, using the Gradient Model (Grujić 2022).
Rq=0.0: RMS surface roughness [m]. Only legal for class 'J'. Only used if sigma (or σ) is also specified. In that case is is used along with sigma to calculate a frequency-dependent sheet impedance using the Gradient Model. The default value of 0 denotes a smooth surface.
disttype::Symbol=:normal: Probability distrubution type for surface roughness. defaults to :normal. The other legal value is :rayleigh.
fufp::Bool: This keyword is not usually required. fufp is mnemonic for "Find Unique Face Pairs". If true, the code will search the triangulation for classes of triangle pairs that are the equivalent in the toeplitz sense. I.e., if triangle pairs (A,B) and (C,D) belong to the same equivalence class, the six vertices in the pair (A,B) can be made to coincide with those of pair (C,D) by a simple translation. If there are many such equivalent pairs, a significant decrease in matrix fill time ensues by exploiting the equivalence. The tradeoff is the time needed to identify them. The default value is true for the strip, diagstrip, meander, manji, loadedcross, jerusalemcross, and 4-sided polyring styles (those employing structured meshes) and false for the remaining styles (those employing unstructured meshes).
save::String="" Specifies a file name to which the sheet triangulation and unit cell data is to be written, typically to be plotted later.

source

PSSFSS.Sheets.read_sheet_data — Function

read_sheet_data(filename::AbstractString)::RWGSheet

Read the sheet geometry data from a JLD2 file named in filename.

source

PSSFSS.Elements.rectstrip — Function

rectstrip(;Lx::Real, Ly::Real, Nx::Int, Ny::Int, Px::Real, Py::Real, units::PSSFSSLength, kwargs...)

Return a variable of type RWGSheet that contains the triangulation for a rectangular strip.

Arguments:

All arguments are keyword arguments which can be entered in any order.

Required arguments:

units: Length units (mm, cm, inch, or mil)
Lx and Ly: Lengths of the strip in the x and y directions.
Px and Py: Lengths (periods) of the rectangular unit cell in the x and y directions.
Nx and Ny: Number of line segments in the x and y directions, for dividing up the strip into rectangles, which are triangulated by adding a diagonal to each rectangle.

Optional arguments:

class::Char='J' Specify the class, either 'J' or 'M'.. If 'J', the unknowns are electric surface currents, as used to model a wire or metallic patch-type FSS. If 'M', the unknowns are magnetic surface currents, as used to model a slot or aperture in a perfectly conducting plane.
dx::Real=0.0, dy::Real=0.0: These specify the offsets in the x and y directions applied to the entire unit cell and its contents. Length units are as specified in the units keyword.
rot::Real=0.0: Counterclockwise rotation angle in degrees applied to the entire unit cell and its contents. This rotation is applied prior to any offsets specified in dx and dy.
Zsheet::Complex=0.0: The frequency-independent surface impedance of the FSS conductor in units of [Ω]. May only be specified for a sheet of class 'J'. If Zsheet is specified, then sigma (or σ) may not be specified. )
sigma or σ: DC, bulk conductivity [S/m]. Only allowed for sheets of class 'J'. Cannot be simultaneously specified with Zsheet. Is used with Rq by PSSFSS to calculate an effective sheet surface impedance at each frequency, using the Gradient Model (Grujić 2022).
Rq=0.0: RMS surface roughness [m]. Only legal for class 'J'. Only used if sigma (or σ) is also specified. In that case is is used along with sigma to calculate a frequency-dependent sheet impedance using the Gradient Model. The default value of 0 denotes a smooth surface.
disttype::Symbol=:normal: Probability distrubution type for surface roughness. defaults to :normal. The other legal value is :rayleigh.
fufp::Bool: This keyword is not usually required. fufp is mnemonic for "Find Unique Face Pairs". If true, the code will search the triangulation for classes of triangle pairs that are the equivalent in the toeplitz sense. I.e., if triangle pairs (A,B) and (C,D) belong to the same equivalence class, the six vertices in the pair (A,B) can be made to coincide with those of pair (C,D) by a simple translation. If there are many such equivalent pairs, a significant decrease in matrix fill time ensues by exploiting the equivalence. The tradeoff is the time needed to identify them. The default value is true for the strip, diagstrip, meander, manji, loadedcross, jerusalemcross, and 4-sided polyring styles (those employing structured meshes) and false for the remaining styles (those employing unstructured meshes).
save::String="" Specifies a file name to which the sheet triangulation and unit cell data is to be written, typically to be plotted later.

source

PSSFSS.Elements.sinuous — Function

sinuous(; arms, b, w, g, sides, ntri, units, s1, s2, kwargs...) --> RWGSheet

Return a variable of type RWGSheet representing a sinuous element as shown in this diagram: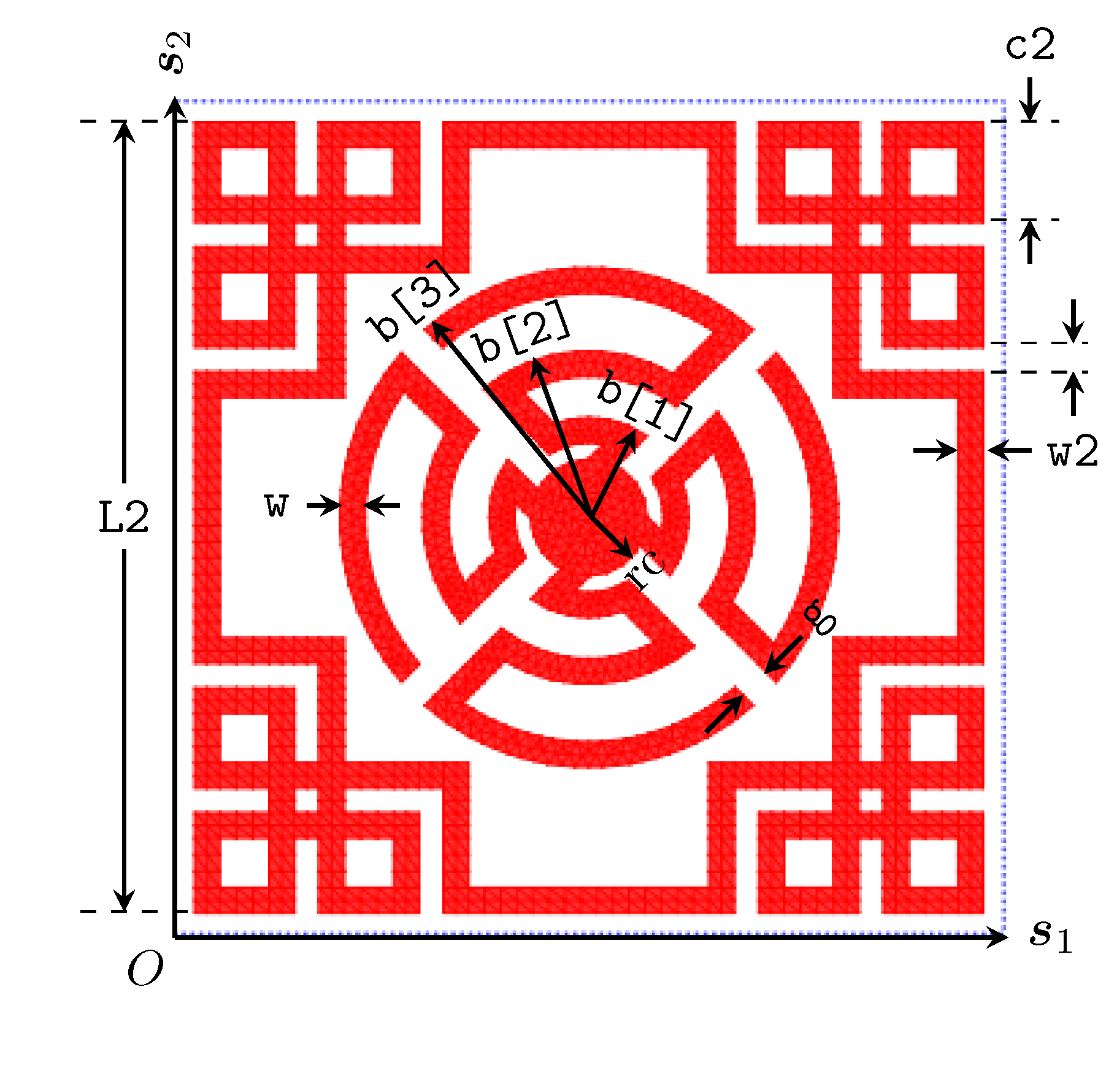

Arguments:

All arguments are keyword arguments which can be entered in any order.

Required arguments:

arms::Int: The number of arms in the structure.
rc::Real > 0: The radius of the central circle. rc must be greater than or equal to w.
b: n-vector (n ≥ 1) providing the outer radii of the polygonal rings. Entries must be positive and strictly increasing, with the difference between adjacent rings exceeding w.
w: The width of the traces in the arms.
g: A scalar containing the rectangular gap width separating adjacent arms.
sides::Int: The number (>= 4) of polygon sides for the background regular annular polygon(s) from which the ring sections are created.
ntri::Int: The desired total number of triangles. This is a guide/request, the actual number will likely be different.
units: Length units (mm, cm, inch, or mil)
s1 and s2: 2-vectors containing the unit cell lattice vectors.

Optional arguments:

orient::Real=0.0: Counterclockwise rotation angle in degrees used to locate center of the first arm.
w2::Real=0.0: The trace width of the enclosing square loop "rim". Note that w2 > 0 is only permitted for a square unit cell.
L2: The outer dimension (i.e. the full side length) of the square "rim" present when w2 > 0. The user is responsible for choosing L2 large enough that the rim does not intefere with the sinuous arms of the structure. L2 must be less than or equal to the square unit cell dimension. It defaults to the unit cell dimension if it is not specified.
c2::Real=0.0: The outer dimension of the small squares shown in the corners of the enclosing square loop "rim". If c2==0 then the squares are not included, and the outer loop is a simple square loop.
class::Char='J' Specify the class, either 'J' or 'M'.. If 'J', the unknowns are electric surface currents, as used to model a wire or metallic patch-type FSS. If 'M', the unknowns are magnetic surface currents, as used to model a slot or aperture in a perfectly conducting plane.
dx::Real=0.0, dy::Real=0.0: These specify the offsets in the x and y directions applied to the entire unit cell and its contents. Length units are as specified in the units keyword.
rot::Real=0.0: Counterclockwise rotation angle in degrees applied to the entire unit cell and its contents. This rotation is applied prior to any offsets specified in dx and dy.
Zsheet::Complex=0.0: The frequency-independent surface impedance of the FSS conductor in units of [Ω]. May only be specified for a sheet of class 'J'. If Zsheet is specified, then sigma (or σ) may not be specified. )
sigma or σ: DC, bulk conductivity [S/m]. Only allowed for sheets of class 'J'. Cannot be simultaneously specified with Zsheet. Is used with Rq by PSSFSS to calculate an effective sheet surface impedance at each frequency, using the Gradient Model (Grujić 2022).
Rq=0.0: RMS surface roughness [m]. Only legal for class 'J'. Only used if sigma (or σ) is also specified. In that case is is used along with sigma to calculate a frequency-dependent sheet impedance using the Gradient Model. The default value of 0 denotes a smooth surface.
disttype::Symbol=:normal: Probability distrubution type for surface roughness. defaults to :normal. The other legal value is :rayleigh.
fufp::Bool: This keyword is not usually required. fufp is mnemonic for "Find Unique Face Pairs". If true, the code will search the triangulation for classes of triangle pairs that are the equivalent in the toeplitz sense. I.e., if triangle pairs (A,B) and (C,D) belong to the same equivalence class, the six vertices in the pair (A,B) can be made to coincide with those of pair (C,D) by a simple translation. If there are many such equivalent pairs, a significant decrease in matrix fill time ensues by exploiting the equivalence. The tradeoff is the time needed to identify them. The default value is true for the strip, diagstrip, meander, manji, loadedcross, jerusalemcross, and 4-sided polyring styles (those employing structured meshes) and false for the remaining styles (those employing unstructured meshes).
save::String="" Specifies a file name to which the sheet triangulation and unit cell data is to be written, typically to be plotted later.

source

PSSFSS.Elements.splitring — Function

splitring(; s1, s2, a, b, sides, ntri, gapwidth, gapcenter, gapangle, units, kwargs...) --> RWGSheet

Return a variable of type RWGSheet similar to a polyring but with zero or more gaps in each concentric annular region.

Arguments:

All arguments are keyword arguments which can be entered in any order.

Required arguments:

units: Length units (mm, cm, inch, or mil)
s1 and s2: 2-vectors containing the unit cell lattice vectors.
a and b: n-vectors (n>=1) of the same length providing the inner and outer radii, respectively of the polygonal rings. Entries in a and b must be positive and strictly increasing. b[i] > a[i] ∀ i ∈ 1:n.
sides: The number (>= 4) of polygon sides for the background regular annular polygon(s) from which the gaps are removed.
gapcenter: A scalar or vector of angles in degrees that define the gap center angular location(s), measured counterclockwise. A scalar implies that all rings have a gap in that same angular location. If a vector, then it must have the same length as a and b, with gapcenter[m] denoting the gap center location for the mth ring. However gapcenter[m] can be either a scalar (denoting a single gap) or an n-tuple (denoting n gaps in the mth ring).
gapwidth: A scalar or a vector of the same length as a and b containing the gap width(s) for each ring. A width of zero implies that the ring is not split (i.e. there is no gap). If the gapwidth of all rings is zero, then the resulting geometry is similar to a polyring. If a ring is to have multiple gaps, then the widths of the gaps for that ring should be passed as a tuple. For example, suppose there are three rings and the second ring has 2 gaps, with the others having a single gap. Then gapwidth = [0.5, (0.4, 0.6), 0.3] would be an appropriately formatted input in this case. When gapwidth is specified, the gaps are implemented as if a rectangular region is removed from the annular polygonal rings. Note that only one of gapwidth and gapangle can be specified.
gapangle: A scalar or vector of the same length as a and b containing the angular widths of the gaps in degrees. As with gapwidth, for any rings with multiple gaps, the corresponding entry in gapangle should be a tuple of the same length as the number of gaps for that ring. When gapangle is specified, the gap(s) in the mth ring is/are formed as if pie-shaped wedge(s) with wedge angle(s) gapangle[m], are removed from the ring(s). The locations and sizes of the tuples in gapangle must agree with those in gapcenter. Note that only one of gapangle and gapwidth can be specified.
ntri: The desired total number of triangles distributed among all the annular regions. This is a guide, the actual number will likely be different.

Optional arguments:

orient::Real=0.0: Counterclockwise rotation angle in degrees used to locate the initial vertex of the polygonal rings. The default is to locate the vertex on the ray from the center parallel to the positive x-axis.
class::Char='J' Specify the class, either 'J' or 'M'.. If 'J', the unknowns are electric surface currents, as used to model a wire or metallic patch-type FSS. If 'M', the unknowns are magnetic surface currents, as used to model a slot or aperture in a perfectly conducting plane.
dx::Real=0.0, dy::Real=0.0: These specify the offsets in the x and y directions applied to the entire unit cell and its contents. Length units are as specified in the units keyword.
rot::Real=0.0: Counterclockwise rotation angle in degrees applied to the entire unit cell and its contents. This rotation is applied prior to any offsets specified in dx and dy.
Zsheet::Complex=0.0: The frequency-independent surface impedance of the FSS conductor in units of [Ω]. May only be specified for a sheet of class 'J'. If Zsheet is specified, then sigma (or σ) may not be specified. )
sigma or σ: DC, bulk conductivity [S/m]. Only allowed for sheets of class 'J'. Cannot be simultaneously specified with Zsheet. Is used with Rq by PSSFSS to calculate an effective sheet surface impedance at each frequency, using the Gradient Model (Grujić 2022).
Rq=0.0: RMS surface roughness [m]. Only legal for class 'J'. Only used if sigma (or σ) is also specified. In that case is is used along with sigma to calculate a frequency-dependent sheet impedance using the Gradient Model. The default value of 0 denotes a smooth surface.
disttype::Symbol=:normal: Probability distrubution type for surface roughness. defaults to :normal. The other legal value is :rayleigh.
fufp::Bool: This keyword is not usually required. fufp is mnemonic for "Find Unique Face Pairs". If true, the code will search the triangulation for classes of triangle pairs that are the equivalent in the toeplitz sense. I.e., if triangle pairs (A,B) and (C,D) belong to the same equivalence class, the six vertices in the pair (A,B) can be made to coincide with those of pair (C,D) by a simple translation. If there are many such equivalent pairs, a significant decrease in matrix fill time ensues by exploiting the equivalence. The tradeoff is the time needed to identify them. The default value is true for the strip, diagstrip, meander, manji, loadedcross, jerusalemcross, and 4-sided polyring styles (those employing structured meshes) and false for the remaining styles (those employing unstructured meshes).
save::String="" Specifies a file name to which the sheet triangulation and unit cell data is to be written, typically to be plotted later.

source